Slope refers to the steepness or incline of a surface or the rate of change of one variable w.r.t another. In various contexts, slope can have different meanings and applications, but its fundamental concept revolves around how things rise or fall relative to distance or time.
Slope plays a critical role in understanding the inclination or gradient of terrain in geography and civil engineering. It helps determine the suitability of land for construction, agriculture, and various other purposes. Roads, railways, and drainage systems are designed with careful consideration of slope to ensure safety and functionality.
In this article, we will explain the slope with the help of definition, formula of slope, methods, and daily life use of slope. Moreover, this article for a better understanding of the slope with the help of detailed examples.
What is Slope?
The slope is the measure of steepness or incline of a line, indicating how much it rises or falls relative to its horizontal distance. In mathematics, particularly in geometry and calculus, slope is most commonly associated with straight lines.
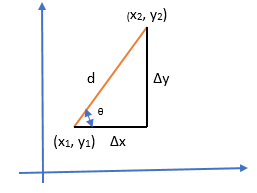
Between two points of any line, the slope represents the ratio of vertical change (rise) to horizontal change (run). This ratio is often denoted by the letter “m” and can be calculated using the formula:
Slope = rise/ run
The slope is the change in y over the change in x. ∆y/∆x = y2 –y1/ x2 –x1
Steps to Find the Slope
In this section, we will discuss the methods used to find the slope of a line between two points.
Identify the Two Points:
Begin by identifying two points on the line. Represent these points as (x1, y1) and (x2, y2).
Use the Slope Formula:
The slope, represented as m, can be found using the following formula: m = y2 –y1/ x2 –x1
Advertisement-X
Here’s how to use the formula:
- For the first point, the coordinates are denoted as x1 and y1.
- For the second point, the coordinates are denoted as x2 and y2.
Determine the Slope:
Subtract y1 from y2 to find the vertical change (rise).
Subtract x1 from x2 to find the horizontal change (run).
Divide the rise by the run to calculate the slope, m.
Interpret the Result:
- Positive Slope (m>0): The line rises as you move from left to right, indicating an upward incline.
- Negative Slope (m<0): The line falls as you move from left to right, indicating a downward incline.
- Zero Slope (m=0): The line is horizontal, meaning there’s no change vertically as you move horizontally.
- Undefined Slope (division by zero): The line is vertical, meaning there is no horizontal change between the points.
Use a Slope Calculator
For those who prefer a quick and error-free method to find the slope, an online slope calculator can be incredibly helpful. Simply input the coordinates of the two points, and the calculator will provide the slope using the formula mentioned above. This tool is especially handy for checking your manual calculations or when dealing with large sets of coordinates.
Examples of finding the slope of a line
Example number 1:
Consider a straight line from a plan. Let’s suppose two points (4,6) and (9,7). Using these points examine the slope.
Solution:
Given data
X1 = 4, X2 = 6 and Y1 = 9, Y2 = 7
Step 1: Formula used to find the slope
Advertisement-X
Slope (m) = Y2 – Y1/ X2 – X1
Step 2: Put all values and determine the slope
Slope (m) = 7-9 / 6-4
Simplify the given data for a better understanding we get.
Slope = -1
Example number 2:
Consider a rise is 20 units and a run is only 14 units. Determine the slope of the line.
Solution:
Given data
Rise = 20 units
Run = 14 units
Advertisement-X
Step 1: Formula for slope rise and run
Slope = Rise / Run
Put the given value of data
Slope = 20 / 14
Slope = 10/7
Daily life uses of slope
The concept of slope is used in various aspects of daily life to describe and analyze different situations. Here are some common daily life uses of slope:
Driving and Navigation: Slope is crucial for drivers and navigation systems. Roads with steep slopes require different driving techniques, and understanding the slope helps drivers anticipate elevation changes and adjust their speed accordingly. Navigation apps also use slope data to provide accurate directions and estimate travel times.
Landscaping: When planning a garden or yard, homeowners and landscapers consider the slope of the land. The slope affects drainage, irrigation, and the choice of plants. Properly managing the slope can prevent erosion and ensure healthy plant growth.
Hiking and Outdoor Activities: Hikers and outdoor enthusiasts rely on slope information to assess the difficulty of trails. Slope steepness is a key factor in trail ratings, and it helps people choose paths that match their skill level and fitness.
Construction and Architecture: Architects and builders use slope data to design structures that conform to the landscape. Understanding the slope helps determine the foundation requirements, accessibility, and drainage solutions for a building site.
Advertisement-X
Gardening and Agriculture: In agriculture, the slope of a field affects water distribution and drainage. Farmers often use contour farming techniques to mitigate soil erosion on sloped land and improve crop yields.
Bicycling: Cyclists consider slope when planning their routes. Uphill slopes require more effort and energy, while downhill slopes offer opportunities for speed. Understanding slope helps cyclists choose routes that align with their goals and fitness levels.
Home Improvement: When installing features like ramps, staircases, or handrails, homeowners need to calculate the slope to ensure safety and accessibility compliance.
Sports: Slope plays a role in various sports, such as skateboarding and BMX biking, where ramps and slopes are integral to the activities.
Weather Forecasting: Meteorologists use slope data to analyze temperature changes with altitude, which is crucial for predicting weather patterns and understanding atmospheric conditions.
Wrap Up
In this article, we have explained the slope with the help of definition, formula of slope, methods, and daily life use of slope. Moreover, this article for a better understanding of the slope with the help of detailed examples.
FAQs
Q. Number 1:
Discuss the meaning of an undefined slope.
Answer:
An undefined slope occurs when the line is vertical, and there is no horizontal change between the points. In this case, the formula for slope results in division by zero, making the slope undefined.
Q. Number 2:
How is slope used in real life?
Advertisement-X
Answer:
The slope is used in various real-life situations, including construction, road design, landscaping, navigation, sports, and agriculture, to assess and manage inclines, gradients, and changes in elevation.
Q. Number 3:
Can slope be negative in a real-world context?
Answer:
Yes, slope can be negative in real-world contexts. For example, a road or hill that descends as you move forward has a negative slope, indicating a downward incline.